The percentage can be divided into 'per-cent-age' which means ‘per every hundred’. It is denoted by the symbol %
Following calculations should be kept in mind:
| \( {1 \over 1}= 100 \% \) |
\( {1 \over 2} = 50 \% \) | \( {1 \over 3} = 33.33 \% \) |
| \( {1 \over 4} = 25 \% \) | \( {1 \over 5} = 20 \% \) | \( {1 \over 6} = 16.66 \% \) |
| \( {1 \over 7} =14.28 \% \) | \( {1 \over 8} = 12.5 \% \) | \( {1 \over 9} = 11.11 \% \) |
| \( {1 \over 10} =10 \% \) | \( {1 \over 11} = 9.09 \% \) | \( {1 \over 12} = 8.33 \% \) |
Comparison between two values of X and Y :
If we compare x to y then we assume y is always equal to 100% When any question asked, what percent of x is y, then y will be written in the denominator.
Q. If x is 80% of y, what percent of x is y?
1st method :
\( y = {100×100 \over 80} x \)
\( y = 125\% {of} x \)
2nd method :
Let y is 100 then x = 80
\(∴ Required \ \% = {100 \over 80}×100 = 125\% \)
Example1 – K is what % of N ?
\[ {K \over N}×100 = {K \over N}\% \]
If A is R % more than B then B is less than A by – $$ {\brack {R \over 100+ R}×100}\% $$
If A is R% less than B, then B is more than A by – $$ {\brack {R \over 100-R}×100}\% $$
Example. If Ram’s income is 10% more than that of Shyam’s income then, how much Percentage Shyam’s income is less than that of Ram’s income?
\( {{10 \over 100+10} × 100} \)
\(
= {{10 \over 110}×100} \) \(= 9 {1 \over 11}\% \)
.png)



















.jpg)








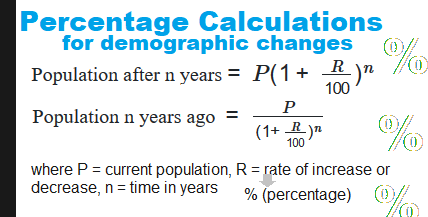 Percentage: Formula And Examples Related To Population
Percentage: Formula And Examples Related To Population