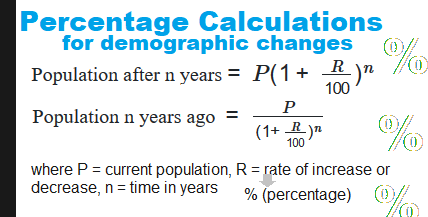In Case of population Increase
Eg. Let the population of a town be p now and suppose increase at the rate of R % per annum then,
Population after n years ( = P (1+{R over 100})^n )
Population n years ago ( = {P over (1+{R over 100})^n})
Example Present population of a town 1.21 crore and it is increasing at 10 % per annum. Then find out the population after two years as well as before 2 years?
Sol. Given, Present population = 1.21 crore,
Two years after
( = P{(1+{R over 100})}^n )
( = 1.21(1+{10 over 100})^2 )
( = 1.21 times 1.21 = 1.4641 crore )
Two years before
( = {P over (1+{R over 100})^n} )
( = {1.21 over (1+{10 over 100})^2} )
( = { 1.21 over 1.21} =1 crore )
In Case of population decrease
Let the population of a town be p now and suppose decrease at the rate of R % per annum then
Population after n year
(= P(1-{R over 100})^n)
Population n years ago
( = {P over (1-{R over 100})^n })
Example: If the present population of a town is 72600 and it is decreased by 10 % per annum. What will be its population 2 years hence?
Sol.
As we Know Population after n year ( = P ({1+R over 100})^n )
Here given,
p = 72600,
R = 10%,
N = 2 years
Population after 2 years
( = 72600({1-10 over 100})^2 )
( = 72600 times{ 90 over 100} times {90 over 100} )
( = 58806 ( Answer ) )
Note : this formula is also used for the depreciation value of machine.
Net % change (= {pm X pm Y pm {XY over 100}} )
‘ + ’ means increment
‘ – ’ means decrement
Example. if the length of a rectangle is increased by 30 % and breadth is decreased by 20 % find the net % change in the area of that rectangle.
Sol. We know that, Net % change ( =
x pm y pm {(x times y) over 100} )
( Let x = 30% ) ( ….( we put x = +30) )
( and y = 20% ) ( …( we put y =-20 ) )
Now net % change
( = +30-20+{((+30) times (-20)) over 100})
(= + 10 – 6 = 4 % )
(
Increase % = 4 % ( Answer) )